
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Astrometry, as you should recall, is the science of measuring POSITIONS of objects in the sky. Not brightness, nor shape, nor color -- just position. It was in many ways the most important aspect of astronomy for thousands of years; not until the late 1800s did the other characteristics of celestial objects start to take precedence.
Several lectures ago, I mentioned the efforts made by astronomers in the past to use astrometry to detect planets circling other stars. The basic idea is that BOTH a planet and its host star will move around their common center of mass.

But we won't see a simple little circle of motion. Because the Solar System, and that other stellar system, are both orbiting the center of the Milky Way Galaxy, the star (and its planet) will appear to drift slowly across the sky, in what we call proper motion.
So, we ought to see a combination of the slow drift and the periodic circles, added together:
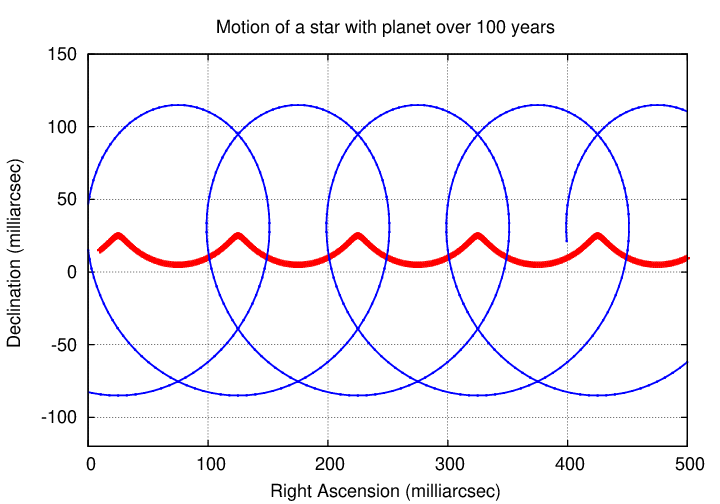
And, of course, in almost all cases, we can only detect the star. The planet is too faint to appear.
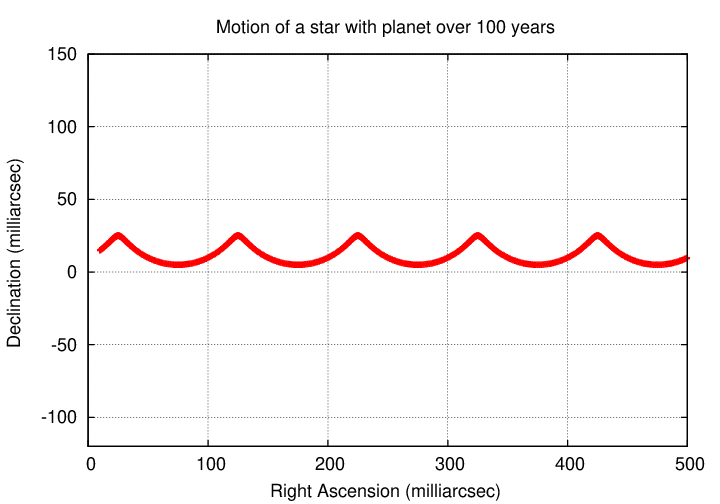
You may also recall that efforts in the 1930s through 1960s to detect exoplanets via this small change in position were unsuccessful. Alas.
Now, when astronomers talk about measurements of the motions of stars in the sky, they sometimes use familiar units: degrees, for example. The Moon moves by about 12 degrees each day; and the Moon itself is about 0.5 degrees across.
But the motions we will consider today are smaller than one degree. Much smaller. Very much smaller. When astronomers discuss such small angles, they choose units which are very small, to match. The basic unit of small angle used by astronomers is the arcsecond.
1 degree = 60 arc-minutes
1 arc-minute = 60 arc-seconds
Q: How many arcseconds are in a single degree?
Q: How many arcseconds across is the Moon?
Arcseconds are really small, which makes them pretty good units to describe our views of planets (and moons) within our own Solar System. The disk of Saturn, for example, is about 15 arcseconds across right now (Nov 2018), while the tiny disk of its moon Titan is only about 0.6 arcseconds across.
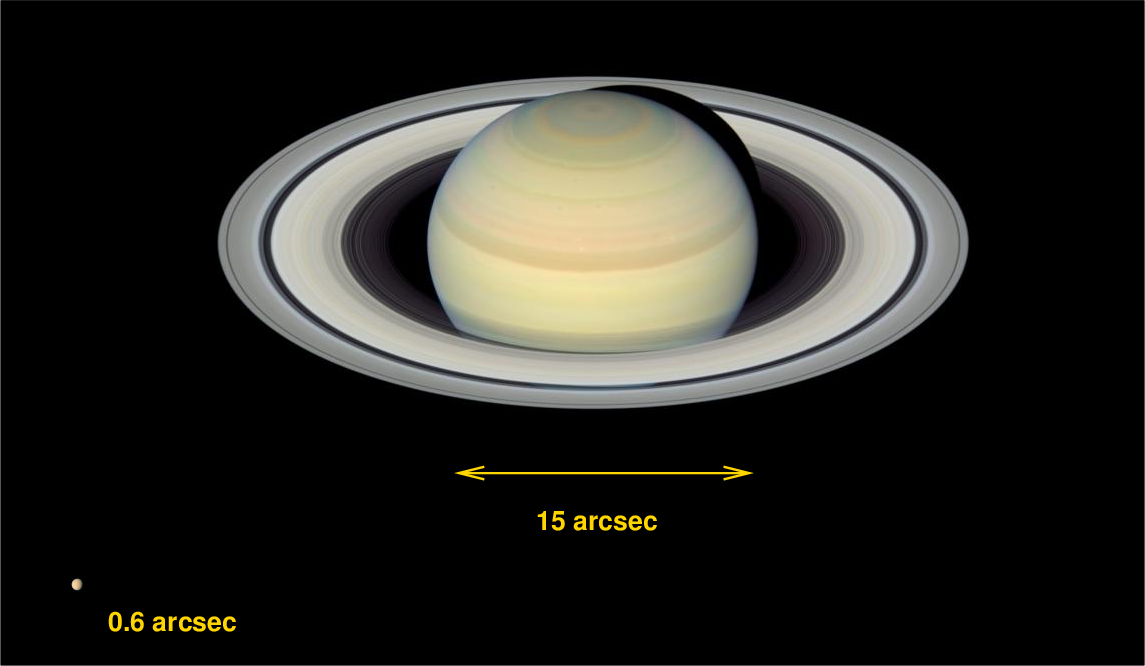
Image of Saturn courtesy of
NASA, ESA and E. Karkoschka (University of Arizona) .
Image of Titan courtesy of
NASA / JPL / Gordan Ugarkovic
But when discussing planets around OTHER stars, or the motions of other stars across the sky, even arcseconds are often too large. We will sometimes use the following in today's discussion:
1 milliarcsecond (mas) = 0.001 arcsecond 1 microarcsecond (μas) = 0.000 001 arcsecond
Okay, set with the units? Let's use them.
"Parallax" is an uncommon word, but it describes a phenomenon you probably have experienced more than once. Let's do a little experiment so that you can experience it once more.
Step 1: Hold your arm out so that it points to the instructor.
Step 2: Close your left eye.
Step 3: Make a fist, then raise your thumb. Move your arm
so that your thumb covers the instructor's head.
Step 4: Open your left eye, close your right eye.
Step 5: Does your thumb still cover the instructor's head?
It shouldn't. You lined up your thumb with the instructor AS SEEN FROM your right eye. If you hold your arm still, and just switch eyes, the thumb won't line up with the instructor any more. The diagram below shows a slightly exaggerated version of the experiment.

What does this have to do with astronomy? Well, the Earth revolves around the Sun, and our telescopes are carried with it. Suppose that in January, when the Earth is on one side of the Sun, a nearby red star, "A", just happens to be lined up with a more distant background star (labelled as "Y"). When we look at the red star "A", we'll see star "Y" next to it.
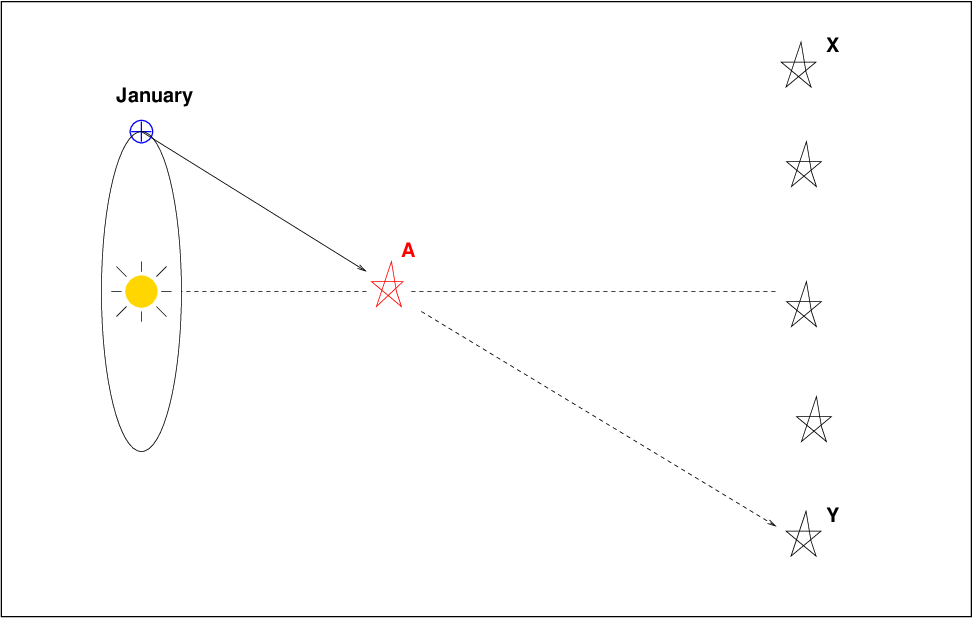
But six months later, in July, the Earth will have moved to the other side of the Sun. If we take a picture of the red star "A" now, it will no longer appear close to the distant star "Y"; instead, it will appear next to the distant star "X".
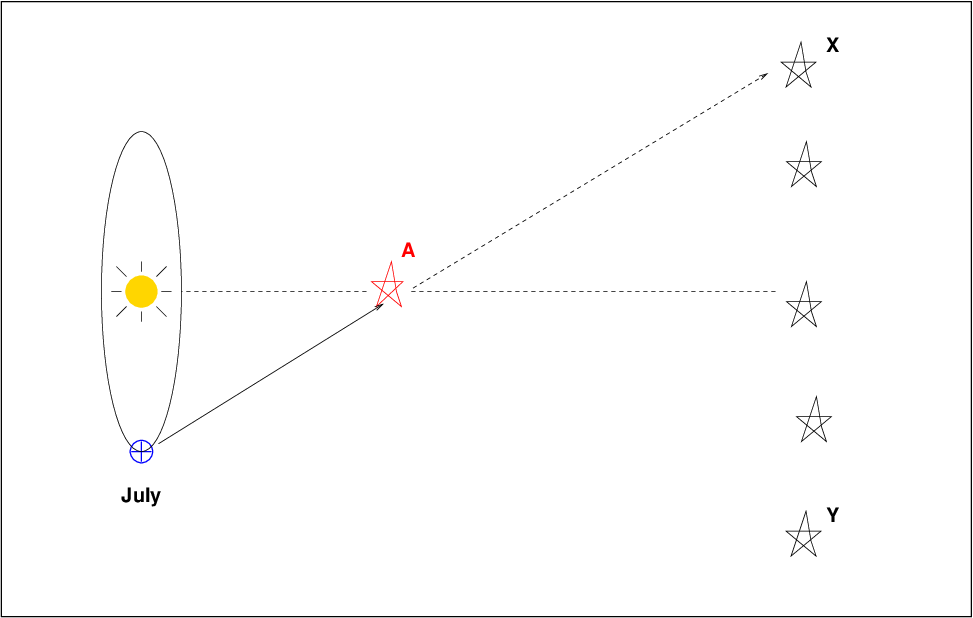
The angle by which the star appears to shift over this six-month period is the parallax angle. It is related to the distance between the Earth and the Sun, R, and the distance L from the Sun to the red star "A", by a bit of trigonometry.

Strictly speaking, the relationship involves the tangent function:
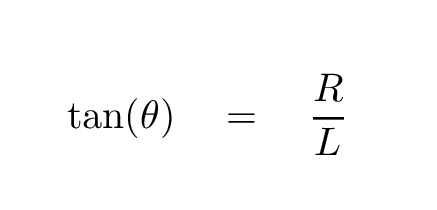
But that's messy, and inconvenient. Fortunately, these angles are all very, very small; and in this special case of small angles, the relationship simplifies.
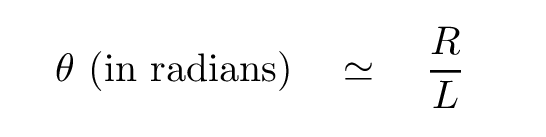
That's better, but we still end up with an equation full of very big numbers: the orbital radius of the Earth is R = 1.5 x 1011 m, and the distances to other stars are typically L = 1017 - 1020 m. Numbers written in exponential notation, with lots of zeroes, are a pain in the neck.
Therefore, astronomers have adopted a set of units which make all the numbers much more easy to handle. If we use
arcseconds for the angle θ Astronomical Units (AU) for the distance R between star and planet parsecs (pc) for the distance L between Sun and nearby star
Then the relationship looks like this:
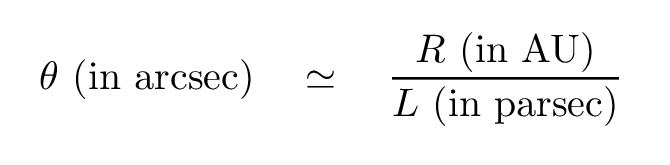
You may be more familiar with describing distances between stars using units of light-years. Well, one parsec is about 3.26 light years.
Let's give this a try. I'll give you the distance to a star, and you tell me the size of the star's apparent shift in position from January to July.
Distance L to star Parallax angle θ
(parsec) (arcseconds)
------------------------------------------------------------
1
5
10
100
100
------------------------------------------------------------
See? Those numbers aren't so hard to read or write.
Now, it is true that no star is as close to the Sun as 1 parsec; and that means that all stars have a parallax angle of less than 1 arcsecond. Just look in your table above. Therefore, to avoid the decimal places, many astronomers choose to describe the angular shift in a star's position due to the Earth's motion using milliarcseconds:
Distance L to star Parallax angle theta
(parsec) (arcseconds) (milliarcsec)
-------------------------------------------------------------------------
1 1 1000
5 0.5 500
10 0.1 100
100 0.01 10
-------------------------------------------------------------------------
Just how big is a milli-arcsecond? I can't just draw an example on the board for you to see from your seats in class, because the lines would be way too close together. So, let's modify things:
The stripe on the board, 5 meters long, is now
being observed by a student in ... Madison, Wisconsin.
According to that observer, the stripe appears to subtend an angle of 1 arcsecond. So, with this new scale, I can now draw a milli-arcsecond: it's about 5 mm wide, as seen from Wisconsin.
Another reason why astronomers choose arcseconds as units for angles has to do with pictures of the stars taken from the Earth's surface. Stars ought to appear as teeny-tiny pinpoints of light, but as the light rays pass through the Earth's atmosphere, the moving air bends them and mixes them and smears them out. The result is that stars appear as little fuzzy blobs in our photographs; blobs with a typical size of about one arcsecond (well, if one is observing from a good site; from Rochester, the blobs are 4 to 5 arcseconds in size. Sigh).
I can put all this information together by showing
you a few simulated pictures I made.

Now, what should we see if we look at a nearby star over the course of many years?
Well, due to the motion of the Earth around the Sun, the star will appear to shift back and forth over the course of one year; and the size of this shift is typically milliarcseconds (maybe 10, maybe 70, maybe 500).
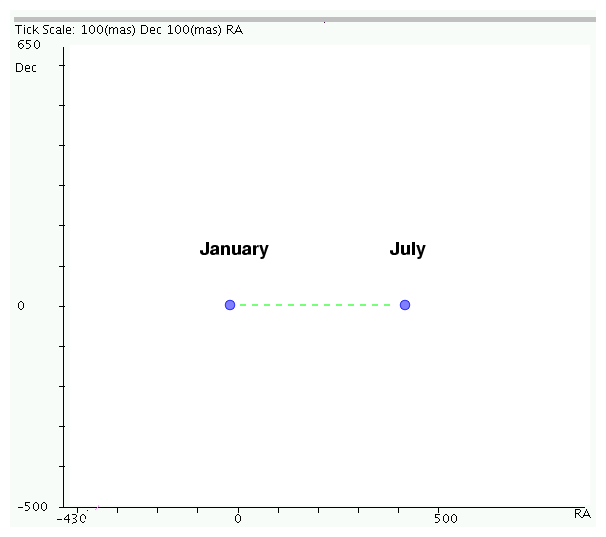
But because the Sun, and the star, are both orbiting around the center of our Galaxy, there will also be a slow drift across the sky -- the proper motion. The result is a combination of a straight-line drift due to proper motion, plus a back-and-forth cycle every year due to parallax.
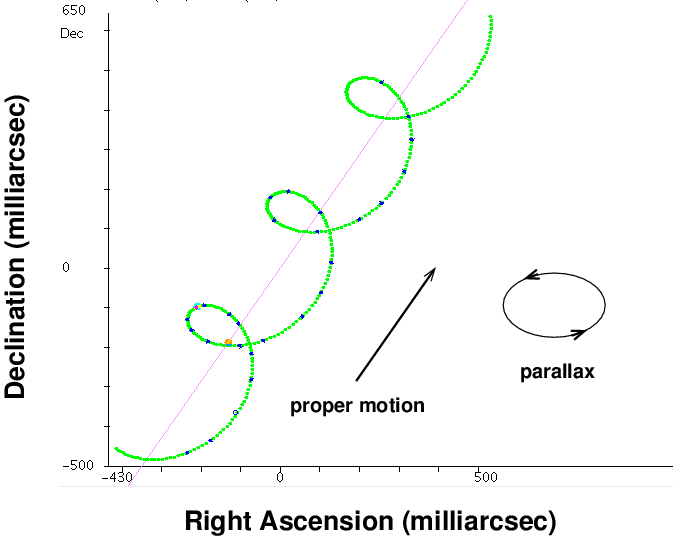
You can make graphs like this using
software at the ESA's Hipparcos tools webpage.
So -- even if a star has no planets of its own, it will appear to move through our sky in a sort of corkscrew-like pattern; and the size of the little twists is typically tens or hundreds of milliarcseconds.
But what if the star DOES have planets? Then the star will wiggle around its center of mass with the planet.
Q: How big will those wiggles due to the planet's influence be?
Hmmm. Good question. We can answer this question in two steps.
First, let's ask "if we could see the planet, how big would its motions around the center of mass be?" Consider this typical situation:
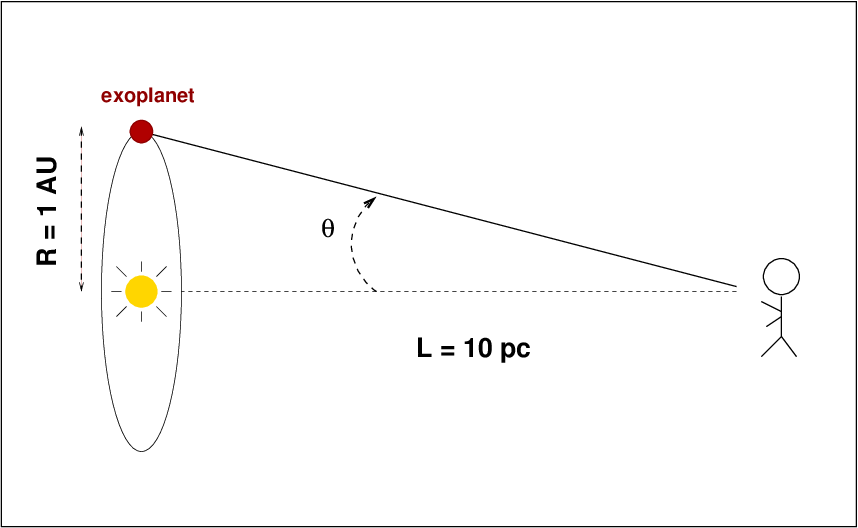
Q: In the situation above, if we COULD see the planet
moving around the star, what would the angular size
of its orbit be?
Yes, nice and easy: the angular size of the planet's motion would be about 0.1 arcseconds, or about 100 milliarcseconds.
But the trouble is that we CAN'T see the planet, in most cases. All we can see is the star. So, we have to look for the tiny motion of the star around its center of mass with the planet. That orbit is much smaller than the orbit of the planet around the center of mass; in fact, the ratio of the sizes of the orbits is the same as the ratio of the masses of star and planet.
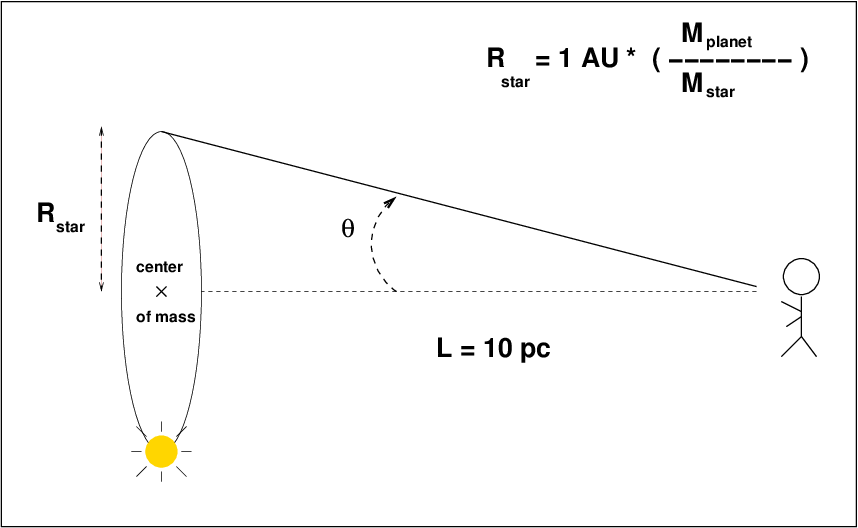
Q: In this example, the star is like our Sun, and the
planet is like Jupiter. The planet orbits at 1 AU
from the center of mass. How far is the star
from the center of mass?
(hint: Jupiter is about 1/1000 of the Sun's mass)
Q: What is the angular size of the star's motion?
That's right: the motion of the star will be 1/1000 the size of the motion of the planet. If the planet's orbit made an angle of 100 milliarcsec, then the star's motion subtends an angle of just 0.1 milliarcsec, or 100 micro-arcsec.
And that's a problem: the motions of even nearby stars due to the gravitational pull of exoplanets is really, really, really small. MICRO-arcseconds instead of MILLI-arcseconds ... and milli-arcseconds are hard enough!
Q: How big is a MICRO-arcsecond?
Well, I'd like to show you, but -- again -- I can't: even if we use the convention that the student watching this class is sitting in Wisconsin, so that the big stripe is 1 arcsecond, I can't draw two lines 1 micro-arcsecond apart.
So, let's move the student farther away. (Click on image to start moving student)
If an observer is sitting in a chair which is about 3 times farther away from the Earth than the Moon, then that observer would see the big stripe on the board subtending 1 milli-arcsecond. And in THAT case, I can draw a pair of lines which represent 1 micro-arcsecond.
The combination of
ends up creating a really complicated, ugly sort of path. Click on the figure to see a short animation.
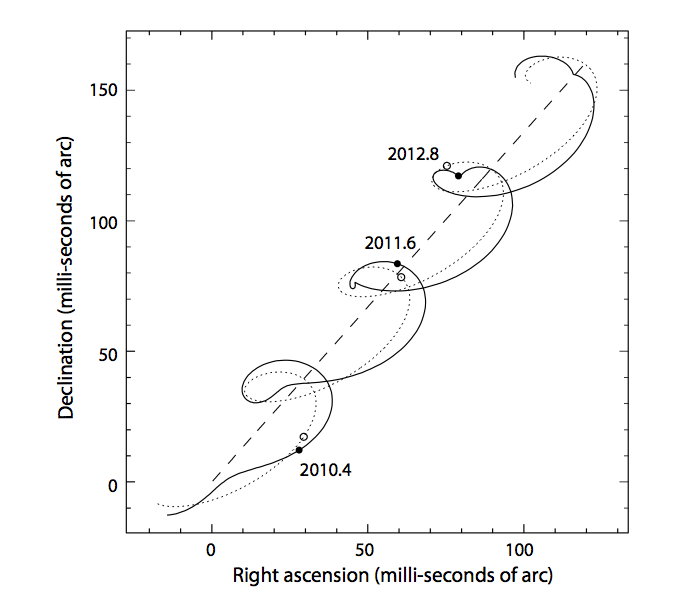
Figure 2 taken from
Perryman (European Physical Journal H, 37, 745 (2012))
In order to detect planets around other stars using astrometry, we need to
That sounds like ... a difficult job.
But Gaia is up to the task! The designers of this satellite made one of its goals to be able to measure positions of stars to a precision of about 10 micro-arcseconds! How did they do it?
Gaia is a rather unusual "telescope," since it has been specially designed for astrometric observations. It resembles the Hipparcos satellite in many ways. The basic structure is built around two triple-mirror telescopes which point at regions in the sky separated by an angle of about 106.5 degrees.
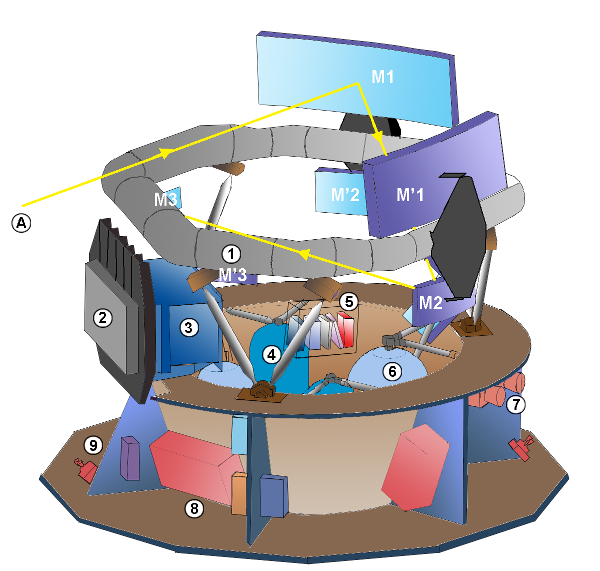
Image courtesy of
Wikipedia
Light from the two telescopes is combined so that it falls upon the focal plane simultaneously. The telescope rotates with a period of six hours, causing stars to sweep across this focal plane in about 60 seconds. Objects in both directions are detected and measured together.
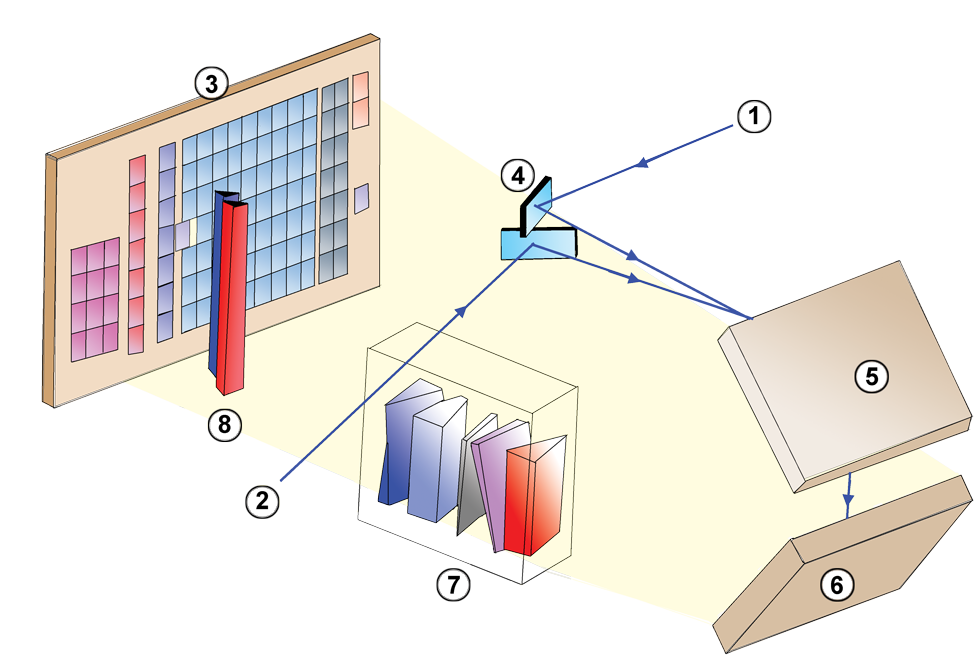
Image courtesy of
Wikipedia
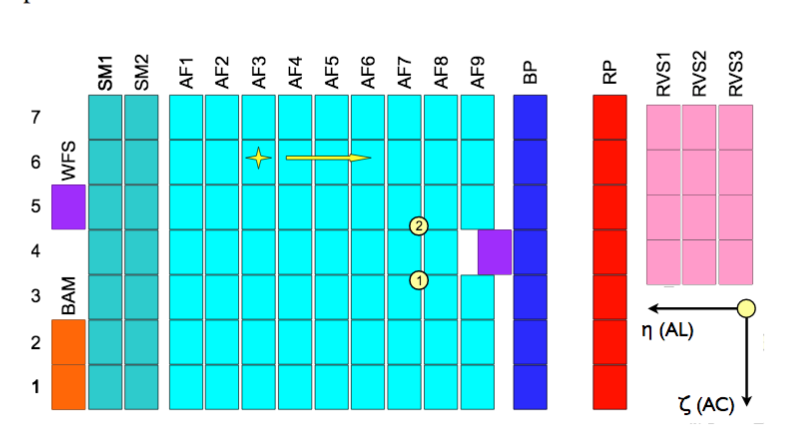
Figure 1 from
Lindegren et al. 2016. Note that this figure
is rotated by 180 degrees relative to previous schematic.
The telescope slowly precesses, so that its spin sweeps out new areas in the sky over time. A typical star will be measured about 70 times over the course of the primary mission (2014 - 2019); that's about 14 measurements per year, though not all equally spaced.
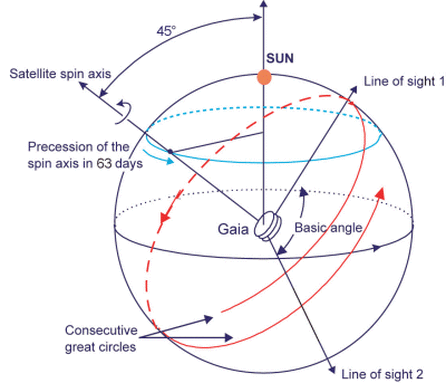
Image courtesy of
Space Flight 101
Click on the picture below to see a video of Gaia's observing procedure .
As the spacecraft precesses, the "partners" of each star will gradually change. Eventually, the spacecraft will have many millions (billions?) of measurements of the relative positions of millions of stars. Scientists can then use a honking-big linear algebra procedure to solve simultaneously for the positions and motions of each star.
How precise are the measurements made by Gaia? A recent paper by de Bruijne, Rygl and Antoja provides some predictions based on the earliest in-flight tests.
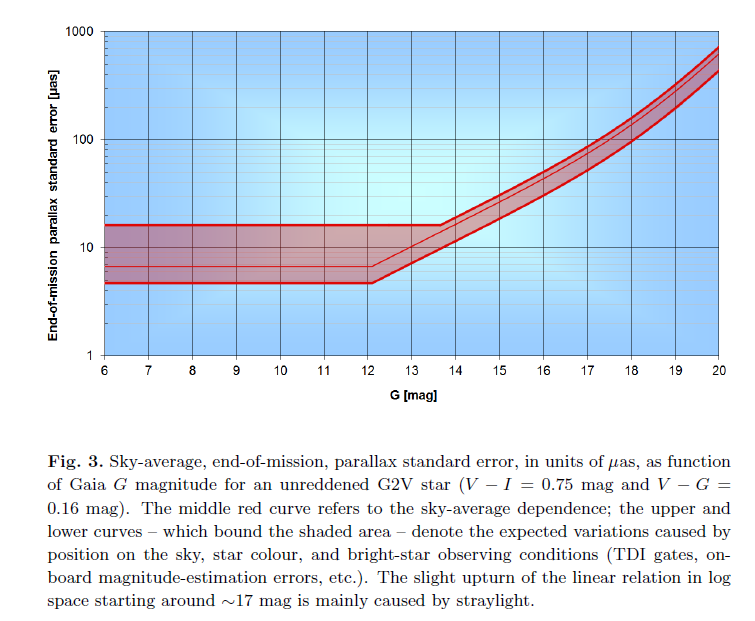
Fig 3 taken from
de Bruijne, Rygl and Antoja (2015)
Q: What sort of planets will Gaia be most likely to detect?
What sort of properties are the planets detected by Gaia likely to have? I've added shaded regions to these diagrams to indicate very roughly the objects to which Gaia should be most sensitive.
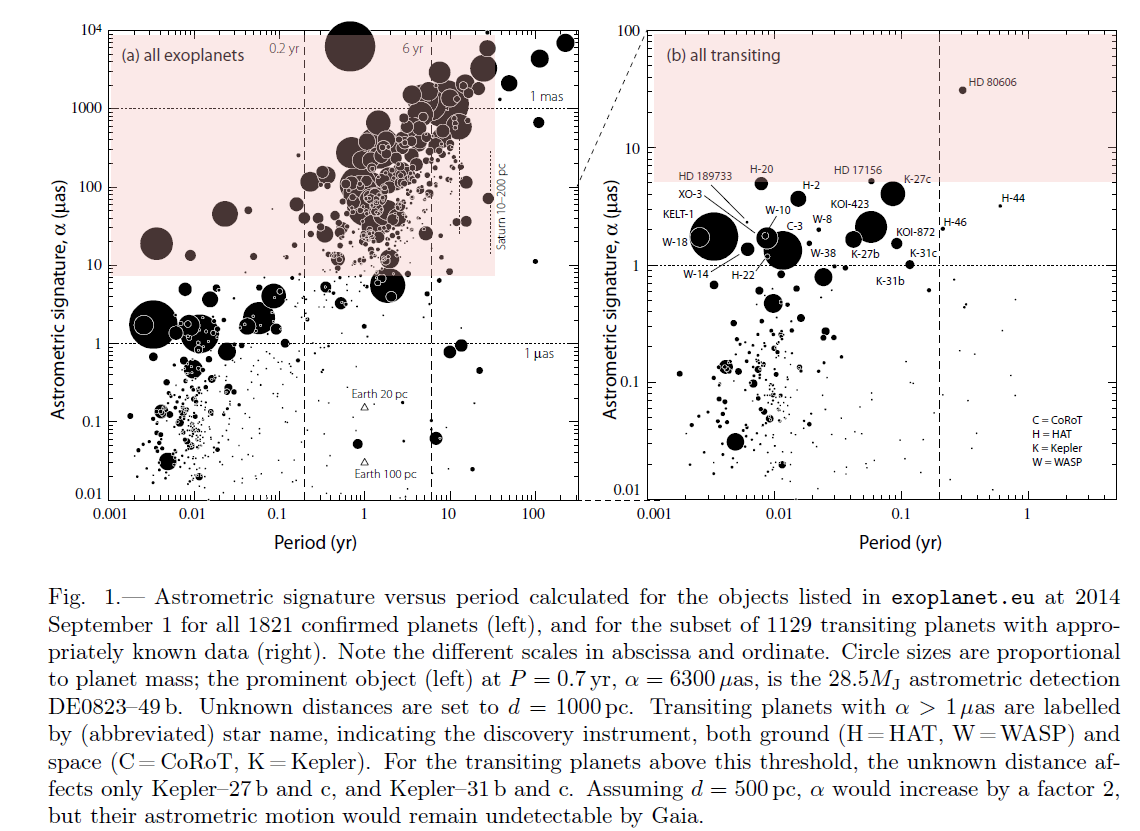
Image modified from Fig 1 of
Perryman et al., 2015
Has Gaia discovered any planets orbiting other stars?
No, not yet.
But that's okay. The satellite is still gathering measurements, and existing measurements are still being processed. The Gaia team won't have the final results -- with the highest precision and longest duration -- for another few years.

Schedule taken from
Data release scenario webpage
on Nov 27, 2018.
There is one Gaia-related exoplanet result: back in the 1990s, an earlier European satellite mission called Hipparcos measured the motion of the star beta Pictoris. It saw the "corkscrew" that one expects, due to proper motion and parallax due to the Earth's orbit around the Sun.

Figure 1 taken from
Snellen and Brown, Nature Astronomy, 2, 883 (2018)
When Gaia measured this star more recently (2013 - 2018), it found that the motion of the star was _slightly_ different than the version measured by Hipparcos. How different?
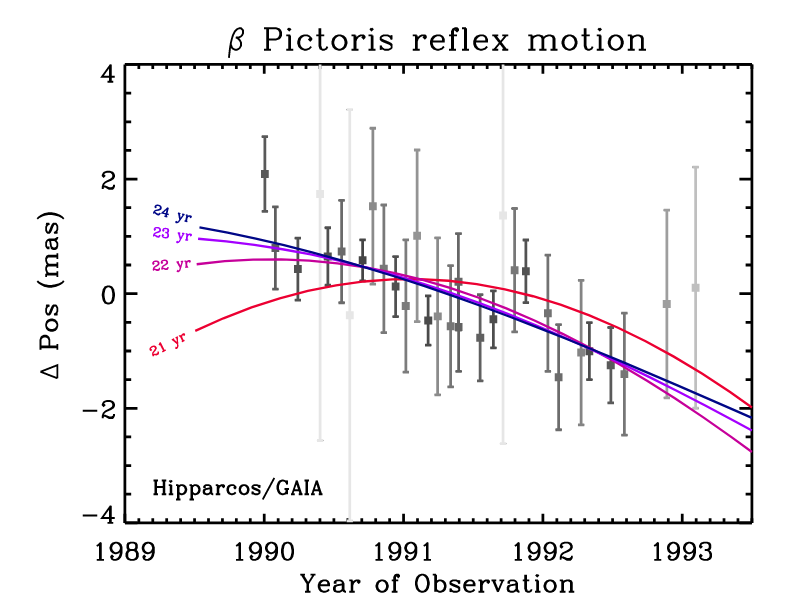
Figure 2B taken from
Snellen and Brown, Nature Astronomy, 2, 883 (2018)
Q: How big are the differences between the expected
and measured position? Look at the vertical scale.
Those differences are just a few milli-arcseconds. But those small differences allow the authors to figure out that a planet with a period of around 21 to 24 years, and a mass around 11 times larger than Jupiter, must be pulling the star.

Taken from the abstract of
Snellen and Brown, Nature Astronomy, 2, 883 (2018)
It may be frustrating to have to wait for Gaia to detect exoplanets ... but, to be far, this wasn't the primary goal of the Gaia mission.
Instead, the main goal of Gaia was to measure the distances to millions of stars, much more accurately than any other survey. Only with accurate distances can we start to make an accurate model of our local region of the Milky Way Galaxy.
Before Gaia was launched in 2013, our best measurements of stellar distances only extended to about 50 pc. That's ... not a big sample of the entire Milky Way.

But after the first Data Release from Gaia, in 2017, we could start to map stars out to about 500 pc. That's a bit better.
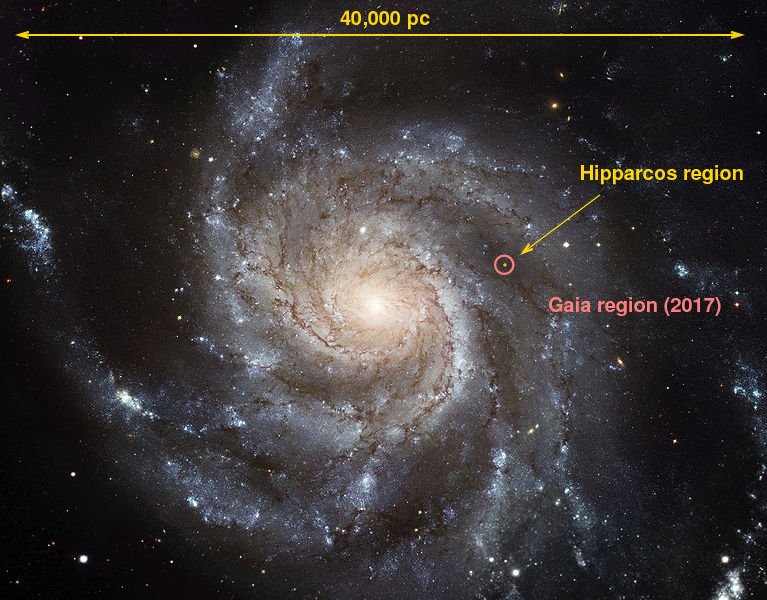
But when the entire mission is complete, in another 4-5 years (?), we can expect to be able to measure accurate distances to stars reaching nearly halfway across the Galaxy!
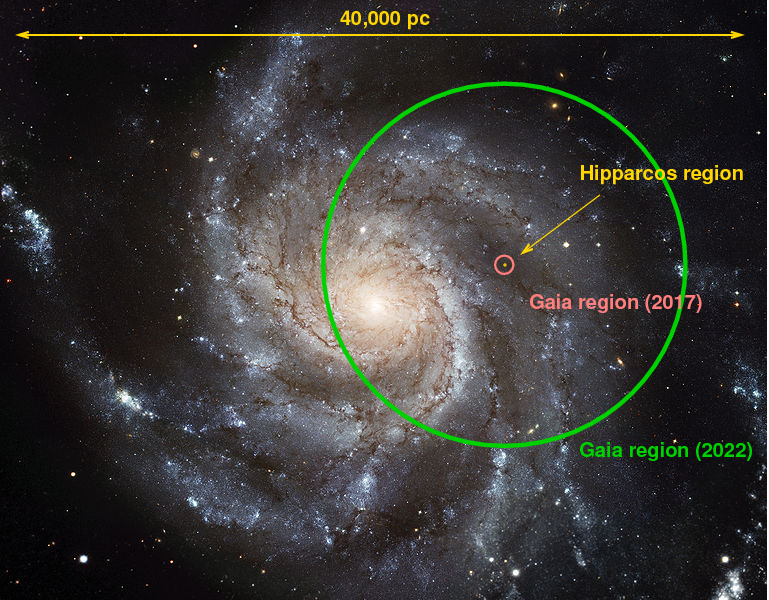
For Gaia, finding exoplanets is just a hobby.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.