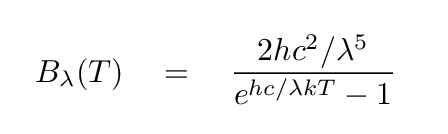
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
What is an X-ray? There are no exact definitions, but most of the astronomical telescopes which call themselves "X-ray instruments" are sensitive to light within this range:
Energy (keV) 0.1 - 500
Wavelength (Angstrom) 100 - 0.02
If a solid, liquid, or dense gas is heated to some temperature, it will emit blackbody radiation. Blackbody radiation has a continuous spectrum which can be described like so
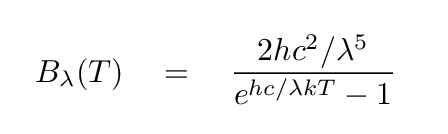
This spectrum has an easily recognizable shape (though it's a bit different when plotted as "flux per unit frequency" and "flux per unit wavelength").
Q: What sort of temperatures are required for a blackbody
to emit significantly in the X-ray regime?
Well, that's a pretty high temperature. Our Sun's photosphere is only about 5,600 Kelvin, and even a really hot star, like theta(1) Orionis C -- the brightest, hottest star in the Trapezium -- has a temperature of only 39,000 Kelvin or so.
Q: Are there any stars hot enough to emit blackbody radiation
in the X-ray portion of the spectrum?
The answer is "yes, but not many." For example, some years after a core-collapse supernova explodes, the dissipating clouds of gas may reveal a very, very hot young neutron star:
Image courtesy of
Adam Block, NOAO and NSF.
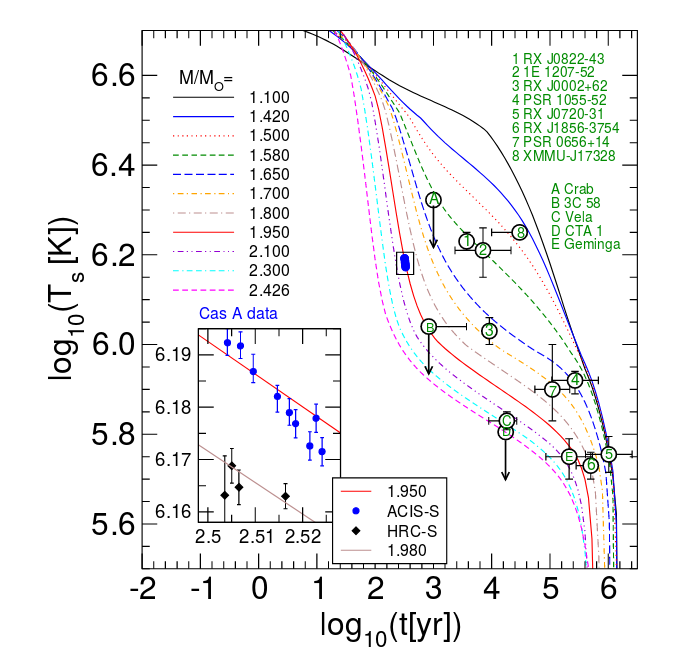
Panel from Figure 3 taken from
Grigorian, Voskresensky and Blaschke, arXiv 1702.01342 (2017)
Way back in the 1890s, when radioactivity and X rays were both new, exciting phenomena, some physicists noticed that if one shot a high-energy electron into a box of stuff, that it would come out the other end moving more slowly; moreover, the stuff would emit a bunch of X rays.
Because it seemed that there was some connection between the slowing down of the electron and the X-ray emission, physicists gave this phenomenon the name "braking radiation". Since most of those involved in this research were German, the word entered our vocabularies as brehmsstrahlung.
What's happening is the result of close encounters between the energetic electron and positively charged nuclei within the material. If the electron passes very close to a nucleus, the mutual electric force will accelerate the electron strongly; and an accelerating charge emits radiation, as we know from our E&M courses.
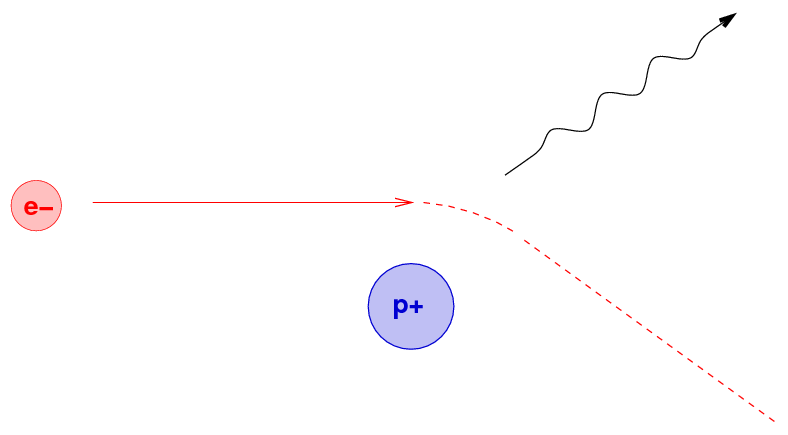
Because the electron might approach the nucleus to within any possible distance, it might end up emitting any wavelength of energy due to a single encounter. As it moves through the material, however, it will interact with numerous nuclei, and so the photons it emits will cover a wide range of energies and wavelengths; in other words, brehmsstrahlung produces a continuous spectrum.
Now, in the 1890s, the source of the energetic electrons was radioactive decay. But out in space, the source of the energetic electrons is often a hot, ionized gas. In that case, the distribution of electron energies is dictated by the temperature of the gas, and so we call the process thermal brehmsstrahlung. In this common case, the emissivity of the gas -- a measure of how much energy it emits per second per unit volume per unit frequency -- can be written as
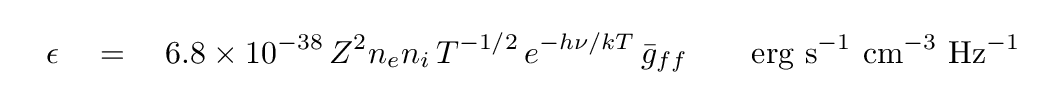
The important features of this emission can be gleaned from the form of the equation.
Q: How does this emission depend on the density of the gas? Q: How does it depend on the temperature of the gas? Q: What happens to the emission as high frequencies?
Consider three clouds of (very) hot hydrogen, at tempertures of 10, 32, and 100 million K. Note how the emission in each case effectively cuts off at certain energy, due to the negative exponential term in the equation.
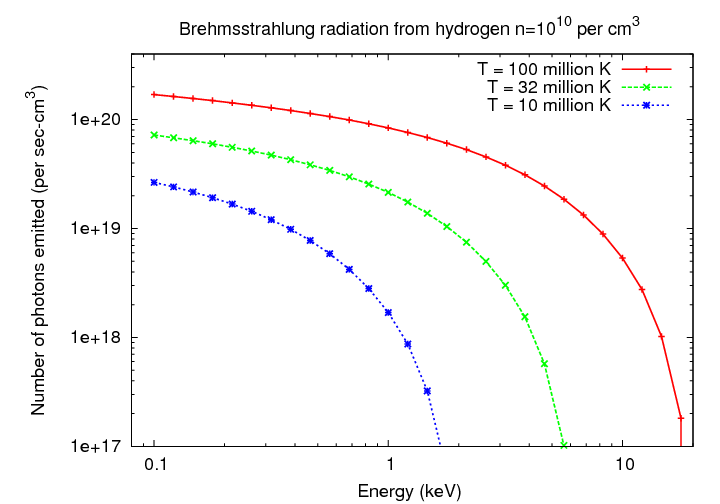
Q: Where can you find clouds of hydrogen at temperatures of
many millions of degrees?
One good source is a rich cluster of galaxies. This cluster, for example, RDCS 1252.9-2927. An optical image shows starlight from the galaxies
Image of RDCS 1252.9-2927 courtesy of
NASA/ESA/J.Blakeslee (JHU)/M.Postman (STScI)/P.Rosati (ESO)
but an X-ray image from Chandra shows emission from the hot gas (purple) filling the space between the galaxies:
Image of RDCS 1252.9-2927 courtesy of
X-ray: NASA/CXC/ESO/P.Rosati et al.; Optical: ESO/VLT/P.Rosati et al.
Another situation in which X-rays might be emitted occurs when a stream of material moving at high speed smacks into a second chunk of material which is NOT moving a high speed.
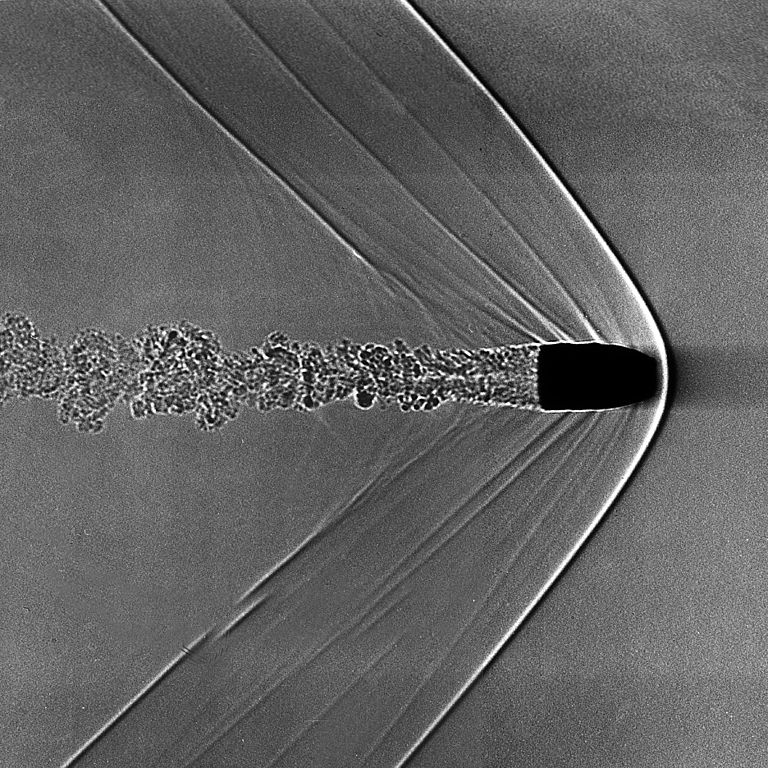
Image of bullet's shock wave courtesy of
Prof. Andrew Davidhazy and Wikipedia
At the interface between the two materials, some very complicated physical processes take place. From our point of view -- a very very very simplified one -- we can consider the bulk motion of material before the collision (bulk kinetic energy) turning into disordered motion of atoms after the collision (thermal energy). Again, the real situation is more complicated.
In general, the material running into a shock with some initial speed vi and low initial density comes out of the shock with a much lower final speed vf and higher final density.
Under certain rather common conditions, for a "strong shock" in which the incoming speed of the gas is much larger than the sound speed of the gas, the final speed is just 1/4 of the initial speed.
Q: A hydrogen atom approaches a strong shock with an
initial speed vi and leaves
with final speed vf = (1/4) vi.
How much of its initial kinetic energy is lost?
The lost kinetic energy can do a number of things. It can dissociate molecules, ionize atoms, excite atoms and ions that remain, and turn into thermal motions of the particles. If the initial speed is high enough, the results can turn into radiation in the X-ray regime.
Let's do an order-of-magnitude calculation to see what sort of velocities are required to reach interesting results. We'll make a number of simplifications:
initial speed (m/s) KE (eV) wavelength Temp (K)
----------------------------------------------------------------------------
100 m/s
1,000
10,000
100,000
1,000,000
-----------------------------------------------------------------------------
Now, one common situation involving shocks and X-ray emission occurs when the stellar wind from a hot star encounters gas in the surrounding interstellar medium. Consider the star zeta Oph, a massive, very hot star of spectral class O9. It is moving rapidly through the surrounding ISM, as this infrared image from Spitzer suggests:
Part of Figure 1 taken from
Toala et al., ApJ 821, 79 (2016)
Chandra X-ray measurements of this region show emission from both gas in an extended region between the star and the bow shock seen in the IR images, and from the location of the star itself.
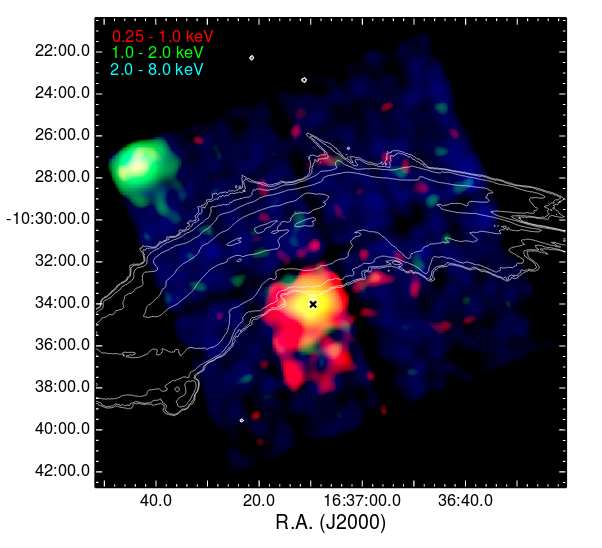
Part of Figure 2 taken from
Toala et al., ApJ 821, 79 (2016)
The spectrum of these X-ray photons looks like this:
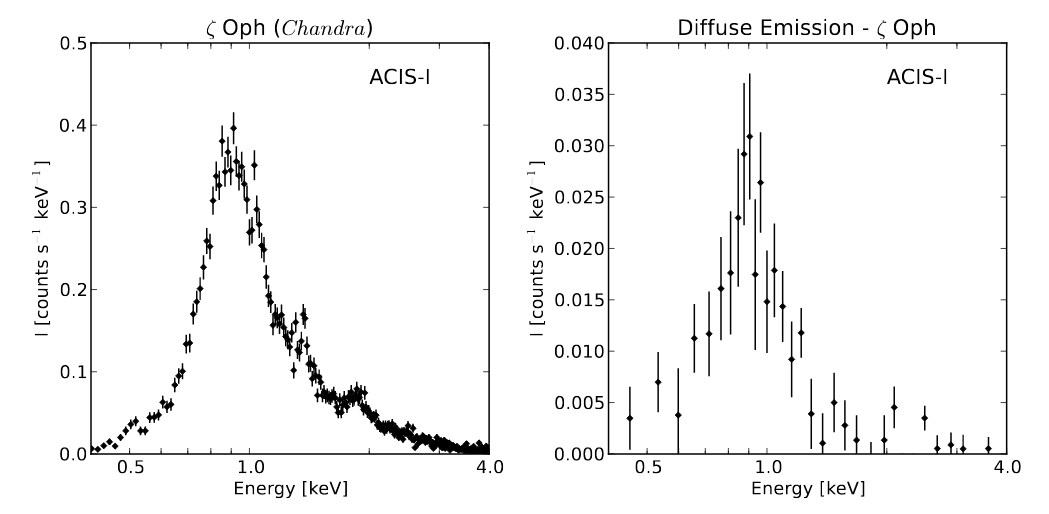
Part of Figure 5 taken from
Toala et al., ApJ 821, 79 (2016)
Q: Suppose the wind of zeta Oph, travelling at speed v,
smashes into the ISM, and all of the kinetic energy
of its atoms are converted into single X-ray photons.
What velocity would the wind have?
The actual wind velocity of zeta Oph, based on more sophisticated analysis ( Marcolino et al., A&A 498, 837 (2009) ), is about 1500 km/s.
Another situation in which shocks can (eventually) produce X-rays is accretion. Imagine a hydrogen atom that falls from a large distance onto a star of radius R and mass M. As the atom falls, its gravitational potential energy (GPE) is converted to kinetic energy (KE).
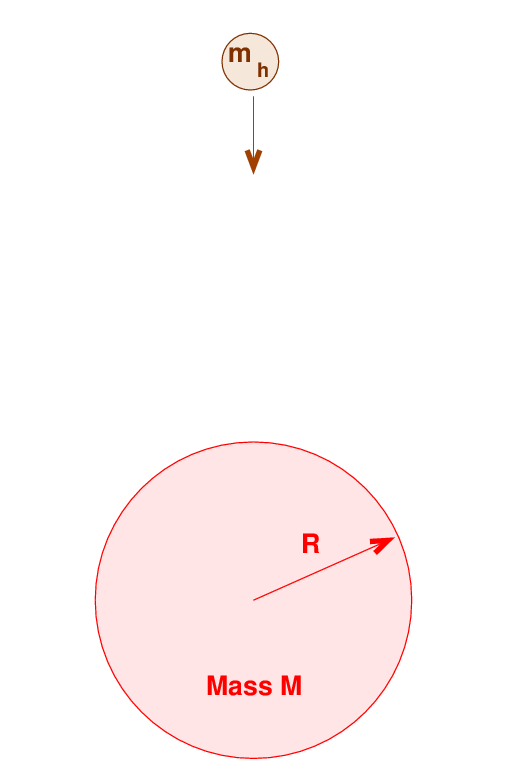
Q: What is the velocity of the atom just as it reaches
the surface of the star? What is its kinetic energy?
Q: Assume that this energy is completely thermalized
in a shock near the surface of the star.
Estimate the temperature of the gas for
a) a star like the Sun
b) a white dwarf star
More sophisticated analyses yield results which are not too different. Mukai (PASP 129, 2001 (2017) , for example, finds this relationship between white dwarf mass and the temperature of material in an accretion shock:
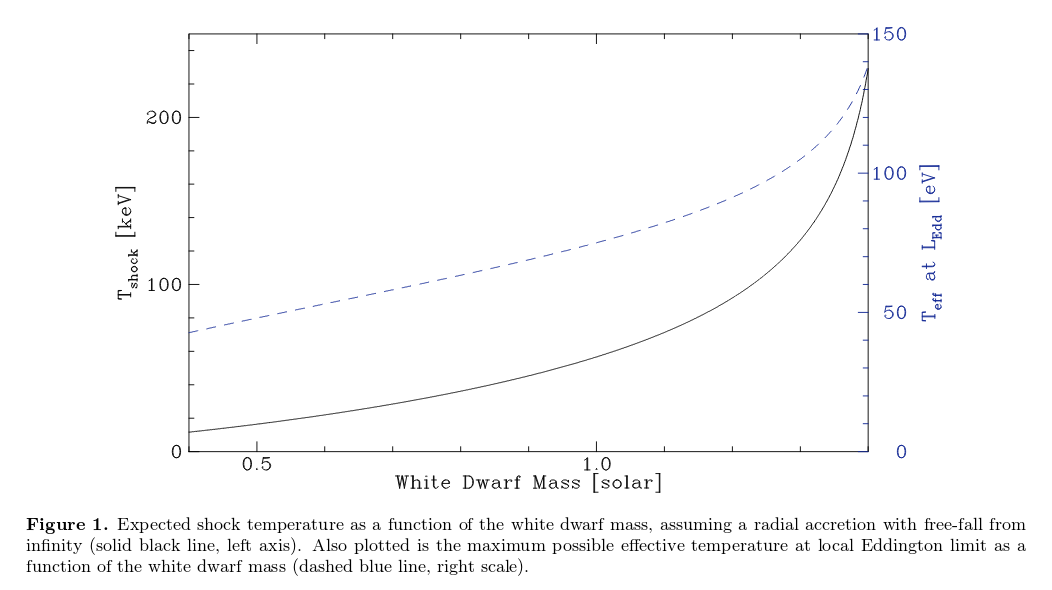
Figure 1 taken from
Mukai (PASP 129, 2001 (2017) ,
You are familiar with line emission from atoms, right? Atoms have quantized energy levels, and an atom in an excited state can drop to a lower-energy state by emitting a photon. In the case of hydrogen, for example, transition from state n=3 to n=2 results in a Balmer-alpha photon.
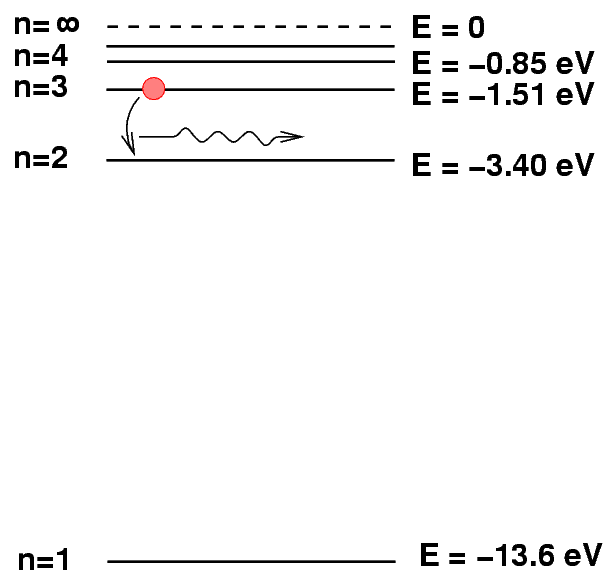
Q: Is it possible for a hydrogen atom to emit an X-ray photon?
No, hydrogen can't emit X-ray photons: the maximum potential energy difference, between the n=infinity and n=1 states, is just (0.0 - (-13.6)) = 13.6 eV.
However, other atoms have more protons in their nuclei, which create a stronger electric potential and the possibility of emission lines with higher energy. For example, consider an iron atom (which has 26 protons) from which 25 electrons have been stripped; in other words, an Fe XXVI ion.
Q: What is the energy of a ground state, n=1, in this atom? Q: What is the energy of the n=2 state in this atom? Q: What is the energy emitted when this atom jumps from n=2 to n=1?
Aha! Now, this sort of transition produces X rays!
In fact, it doesn't have to be this extreme a case. If any common (in space) atom, such as oxygen or carbon, should sit in an environment in which
then that atom may produce photons in the UV or X-ray range.
The star T Pyx is a recurrent nova: a white dwarf star in a close binary orbit with an ordinary companion. The white dwarf accretes material from its companion, building up a layer of hydrogen on its surface. Every few decades, conditions at the bottom of this thin layer of hydrogen become just right for fusion reactions to begin. BOOM
During the weeks that follow these nova explosions, material blown off the star's surface is very hot. Tofflemire et al. (ApJ 779, 22 (2013) provide measurements of this gas from the 2011 explosion of T Pyx:
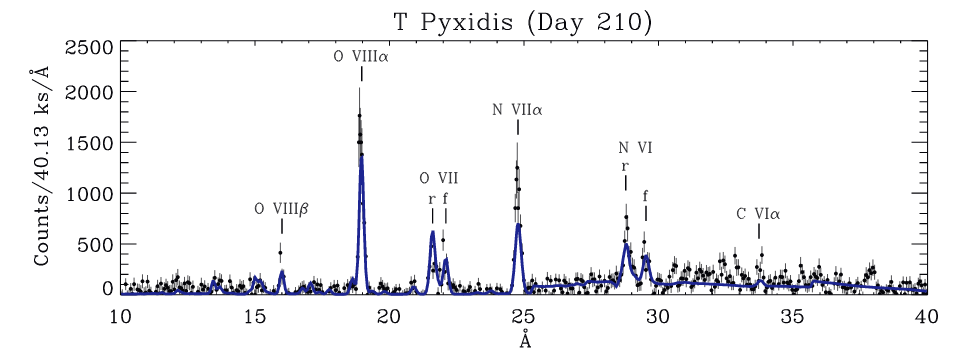
Taken from Figure 2 of
Tofflemire et al. (ApJ 779, 22 (2013)
Q: Note the line labelled "O VIII alpha" in the spectrum above.
It represents the n=2 -> n=1 transition of a seven-times-
ionized oxygen atom.
What _should_ the wavelength of this transition be?
What is the wavelength in this spectrum?
Of course, some atoms have more than 1 electron left, even in very hot environments. The spectrum above shows a line of oxygen as O VII, which has 2 electrons. When an atom has two or more electrons orbiting its nucleus, the energy levels are not so simple to calculate, due to the interactions of the electric fields between the electrons.
One case that is still pretty simple is that of the K-shell electrons in iron. Atoms with high atomic number (many protons in their nuclei) have electrons arranged in shells; you may recall something from a chemistry or physics course that drew a connection between these shells and the periodic table of the elements.
The innermost shell of electrons is called the "K shell", and can contain just two electrons. These tightly-held electrons have energy levels which are close to those of simple hydrogenic atoms, but just a bit smaller; they behave as if their nuclei have (Z - 1) protons, due to shielding by the other K-shell electron.
Q: Compute the energy of the n=1 state for an iron K-shell electron.
Q: Compute the energy of the n=2 state for an iron K-shell electron.
Q: If a K-shell electron drops from n=2 to n=1, what is the energy
of the emitted photon?
When we look at the accretion disks around supermassive black holes, we sometimes see one strong emission line at something close to this energy:
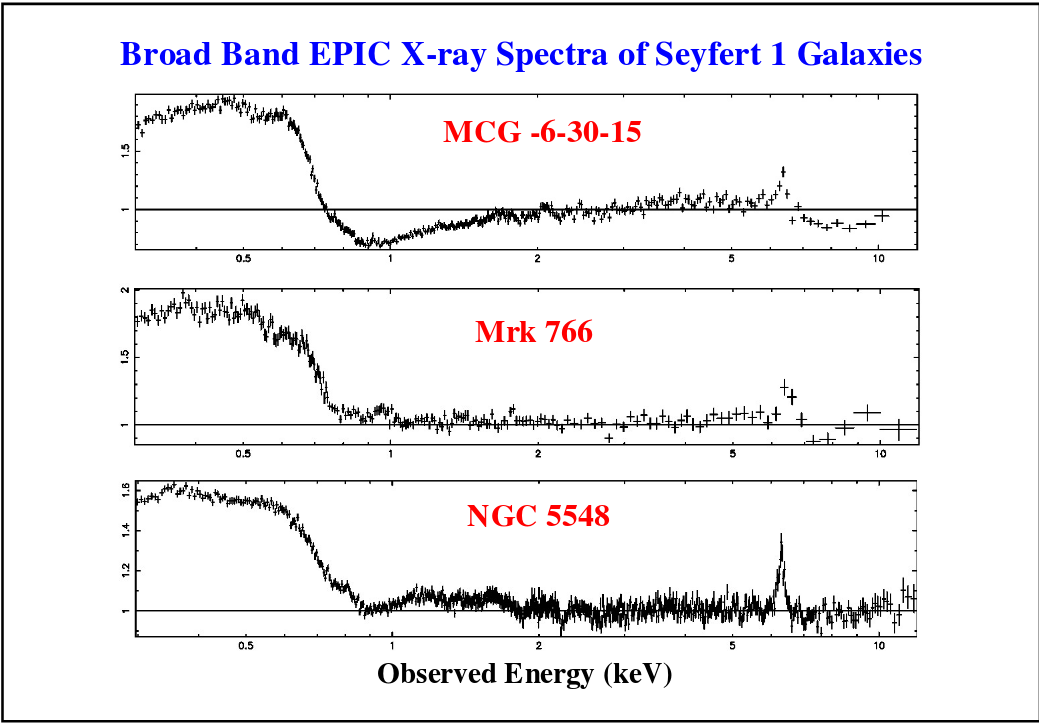
Image taken from
a presentation by James Reeves
It might be possible to use the detailed shapes of the K-alpha emission lines in AGN to derive properties of the black hole itself!
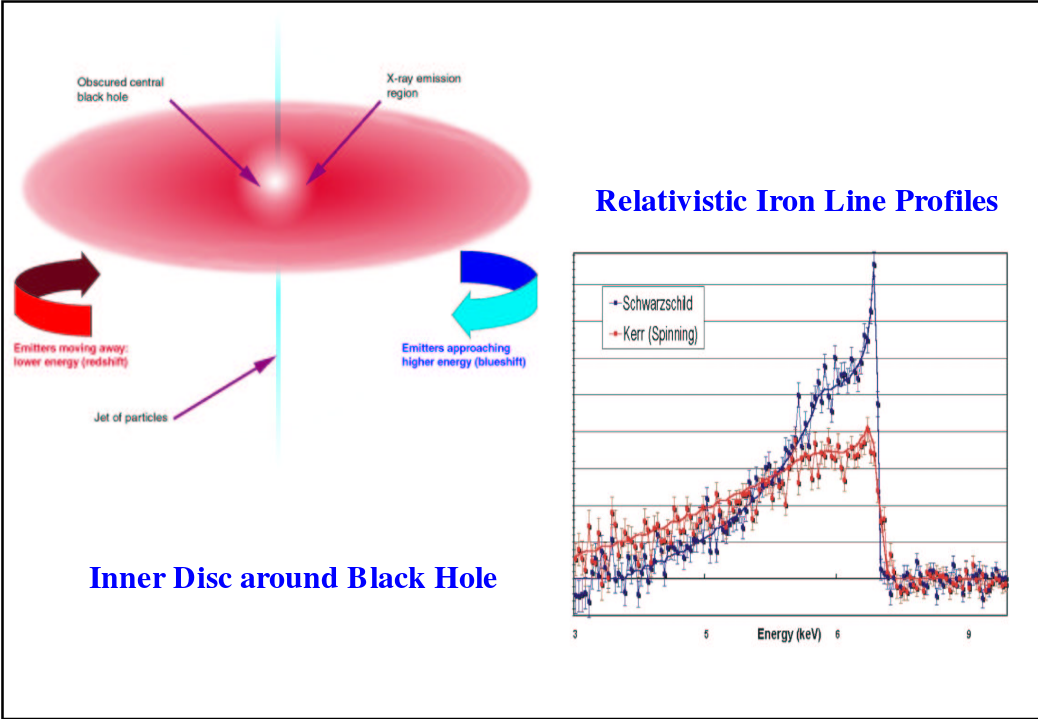
Image taken from
a presentation by James Reeves
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.