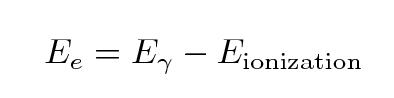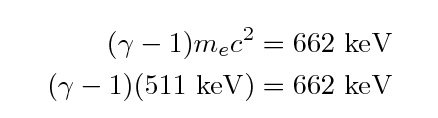Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Counting gamma rays with a scintillation detector
Let's take a look at how a scintillation detector works.
How does it convert a gamma ray into an electrical pulse
that can be counted?
When a gamma ray approaches an atom, there are several
things that can happen.
- The gamma ray may not interact at all -- which is
rather uninteresting, so let's skip that.
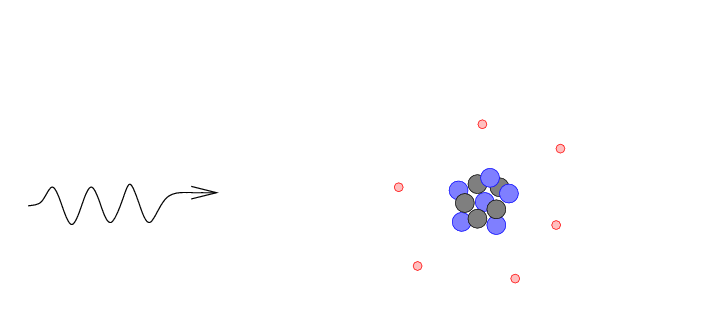
- The gamma ray may be absorbed by the atom,
giving its energy completely to an electron
which is consequently knocked out of the
atom. This is a photoelectric absorption.
- The gamma ray may transfer some, but not all, of its
energy to an electon, again knocking it free
from the atom. This is Compton scattering.

One can use conservation of energy and momentum to
derive formulae for the energy of the gamma-ray and
the electron after an episode of Compton scattering:
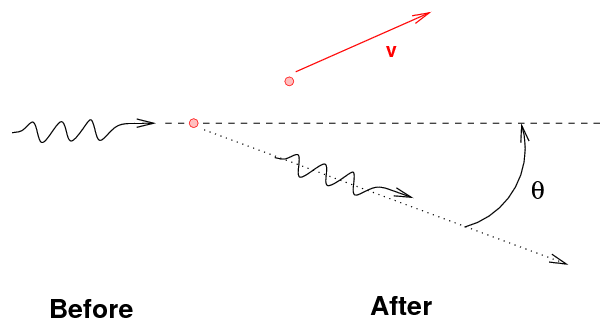
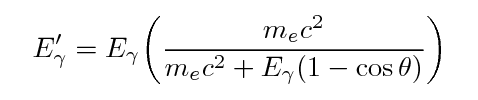
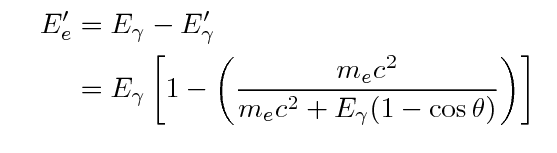
Note the general result: the gamma ray always has
less energy than it started, but there is an upper limit
to the amount of energy it can lose.
That means that the energy of the ejected electron
may range from zero to a maximum value, which is
again less than the energy of the incoming gamma ray.
- The gamma ray may interact with the nucleus.
We won't consider that case here.
Let us concentrate on possibilities 2 and 3.
We'll begin with photoelectric absorption.
The energy of the freed electron must be
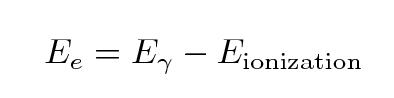
In our lab, some typical values are
- gamma ray energies of 500 to 1200 keV
- ionization energies of 1-10 eV (sodium 5.1 eV, iodine 10.4 eV)
so it should be clear that the energy given to the liberated
electron is almost exactly the same as the energy of the
incident gamma ray, to a tiny fraction of a percent.
So, at this point, we have one electron with a boatload of kinetic
energy. How can we turn this into a signal we can detect?
The answer is to convert the electron's kinetic energy into visible light.
The mechanism involves many collisions with atoms in a
special sort of crystal:
sodium iodide, doped with a small amount of thallium
to replace a small fraction (0.1% to 0.4%) of the sodium atoms.
The function of the thallium is to modify the electronic properties
of the crystal.
In an pure sodium iodide crystal, one finds the usual
situation: a valence band and a conduction band,
separated by a large gap,
in this case about 5.9 eV.
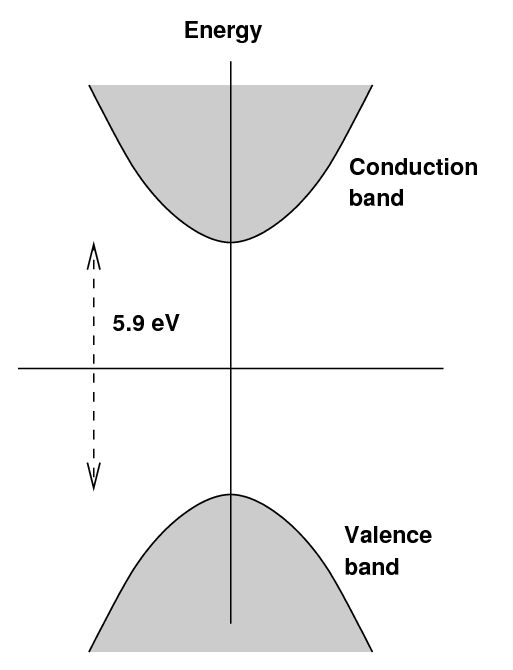
If an electron were excited into the conduction
band, then managed to drop back down into
the valence band by emitting energy as a photon,
the wavelength of that photon would be around 210 nm,
in the near-UV.
Such a photon would immediately be absorbed by
other atoms in the crystal,
which would prevent it from leaving the crystal
and being measured.
When a small amount of thallium is added to the crystal,
new bands are created at a somewhat lower energies
above the valence band.
The term "exciton" is sometimes used to describe
electrons in this state.
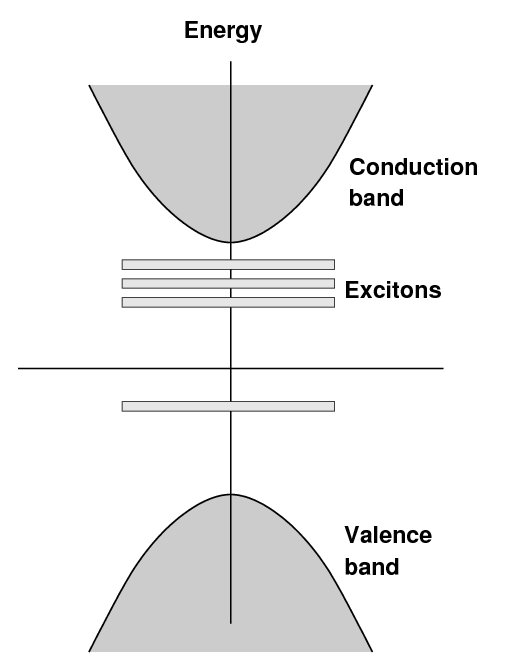
An electron excited into the conduction band
may now drop down to the lowest energy in
the conduction band (as usual), but
now it may drop further by small steps into
the exciton states.
As the electron makes its way back to the
valence band by these small steps,
it may emit a photon with a lower energy
and longer wavelength.
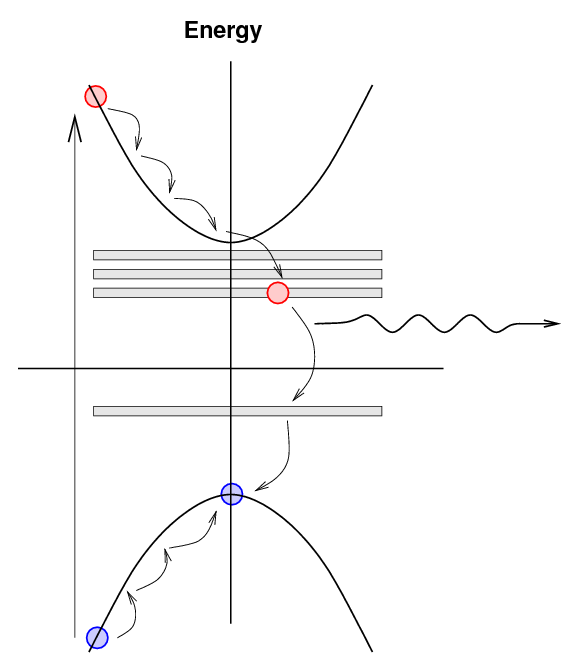
The lower energy and longer wavelength of this
photon are important for the detection process
in two ways:
- This photon can travel much farther through the
crystal before it interacts with other atoms,
since it does not have enough energy to
bump electrons out of the valence band
into the conduction band.
In the case of sodium iodide, the
free path length of this photon may be
several centimeters,
versus micrometers or less for a 5.9-eV photon.
- This visible-light photon may be detected more
efficiently by common photosensitive devices
such as photomultiplier tubes.
In the case of sodium iodide, these
exciton-based photons have wavelengths
of roughly 350-500 nm, or energies of roughly 2.5-3.5 eV.
- How many photons will be emitted for each gamma-ray?
-
Most of the kinetic energy of the initial electron is NOT
converted into visible light. Instead, most of that kinetic
energy is turned into heat as the electron bumps into
atoms in the crystal.
Only about 10 percent of the electron's kinetic energy
eventually emerges as photons.
Since each photon carries about 3 eV, we can figure out
very roughly how many photons will be created from a single
gamma ray.
initial gamma ray E = 662,000 eV for Cs-137
x 10 percent = 66,000 eV
/ 3 ev/photon = 22,000 photons
So, each gamma ray may cause tens of thousands of
visible-light photons to be emitted from the crystal.
Remember that only a fraction of these photons will
go in the right direction -- towards the photomultiplier tube.
- How long does it take for the electron to lose its energy?
-
We'll do a very rough estimate here, just to get the order
of magnitude.
Begin with the initial speed of the electron.
We can use the formula for relativistic kinetic energy to
figure out the gamma factor for the electron:
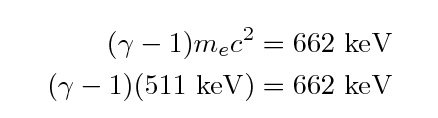
We find that gamma = 2.3 and so the initial velocity of the
electron must be around v = 0.9 c, very close to the
speed of light.
At relativistic speeds, it takes only around 10-18
seconds to travel from one atom in a crystal to another.
Even if the electron must travel many atoms between interactions,
it can make tens of thousands of collisions in a very short time,
perhaps 10-13 seconds.
- How long does it take for excited atoms to generate a photon?
-
The decay time for an exciton (excited location in the crystal lattice)
is around 250 nano-seconds for sodium iodide with thallium doping.
This is so much longer than the time required for the initial
electron to dump all its energy into the crystal lattice
that, for practical purposes, all the photons due to a single
gamma-ray will be emitted simultaneously.
So, we can see how a single gamma-ray produces many thousands
of photons of visible light.
Some of these photons are detected by a photomultiplier tube.
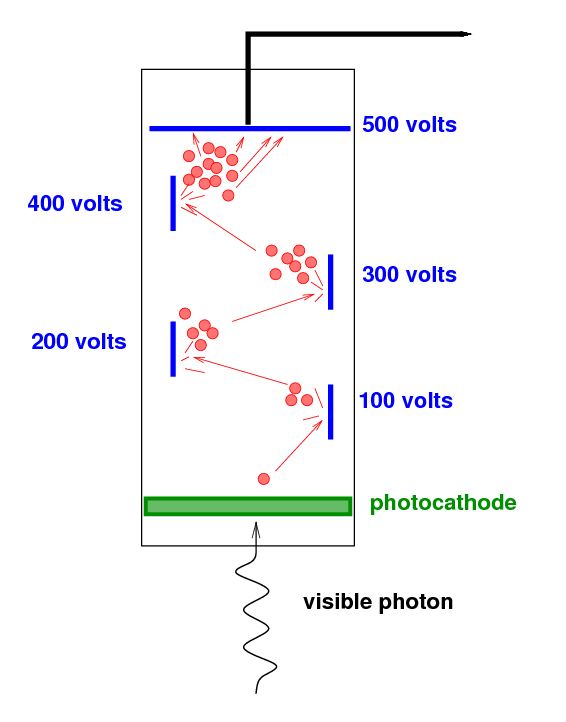
The incoming visible photon knocks just one electron from
the photocathode.
That single electron is accelerated through a high voltage,
causing it to strike a metal surface (a "dynode") at high speed.
It knocks several electrons free, and they
are in turn accelerated towards a second metal surface.
This process is repeated a number of times,
increasing the number of electrons at each stage.
By the end of the photomultiplier tube,
the single electron has turned into a cloud of many thousands
of electrons,
a signal which can easily be measured.
The size of each packet of charge striking the final
dynode (the anode) in a photomultiplier tube
indicates the number of photons which struck
the photocathode;
that, in turn, indicates the energy of the
electron which was bumping into atoms in the
crystal;
that, in turn, indicates the energy of the original gamma ray.
There are, after all, quite a few steps in the process:
- a gamma ray strikes at atom in the crystal, giving
one electron much of its energy (hundreds of keV)
- this high-energy electron strikes many other atoms
in the crystal, creating many electron/hole pairs
- some of the electron/hole pairs recombine via excited
states at special sites in the crystal; each such recombination
yields one visible-light photon
- some of the photons leave the crystal and strike
the photocathode of the detector,
knocking one electron free
- the liberated electrons are accelerated inside the
photomultiplier tube before striking
a dynode and knocking free multiple electrons
- repeat last step 5-10 times
- a large cloud of electrons strikes the anode of the
photomultiplier tube,
giving it a negative charge which can
be measured by a capacitor
Features in a gamma-ray spectrum
So, when we look at the spectrum of a typical gamma-ray source,
such as Cs-137,
what should we expect to see?
If we had a PERFECT instrument, we might expect to see
a spectrum like this:
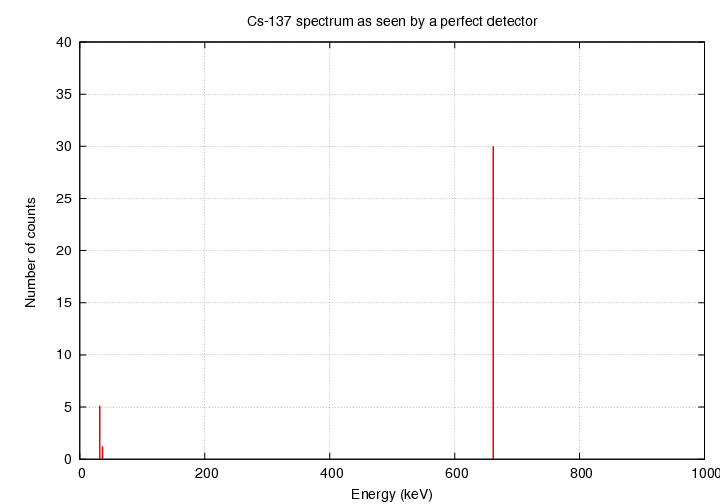
since Cs-137 produces gamma rays with energies of
32.06, 36.40 and 661.7 keV.
But what we ACTUALLY see looks quite different:
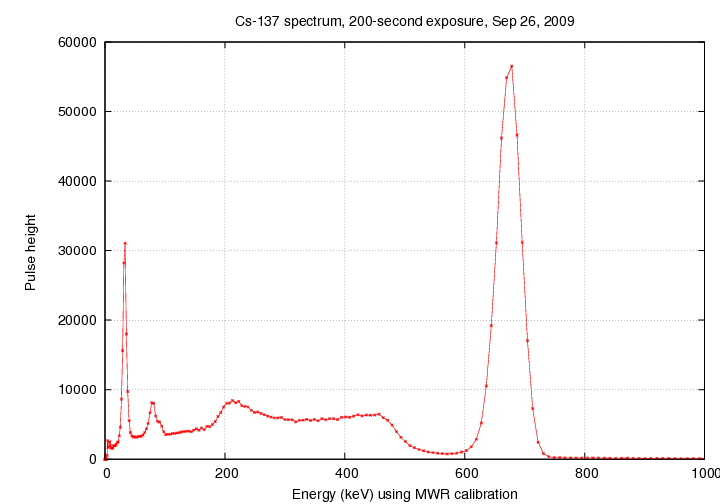
What has happened?
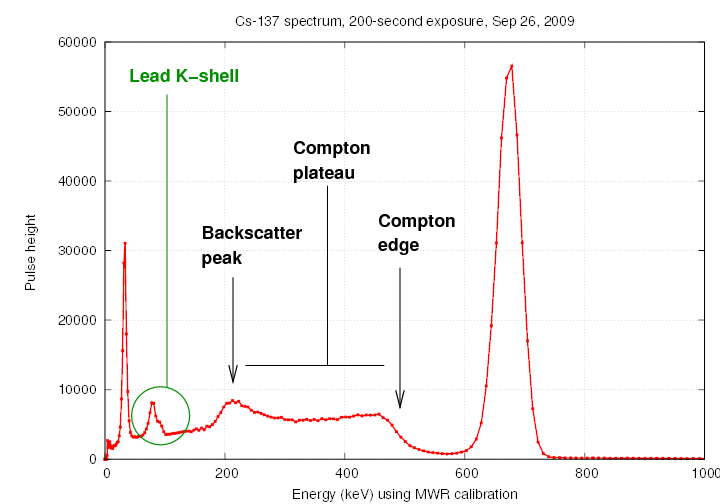
We usually place the radioactive source
in the middle of a little structure made of lead bricks,
to prevent radiation from escaping into the room at large.
Some of the gamma rays from the source interact with the
lead atoms in the bricks, creating lower-energy scattered
gamma rays and also X-rays with the characteristic
energy of the L-shell-to-K-shell transition in lead.
The interactions with the lead shielding lead to several
noticeable features in the spectrum.
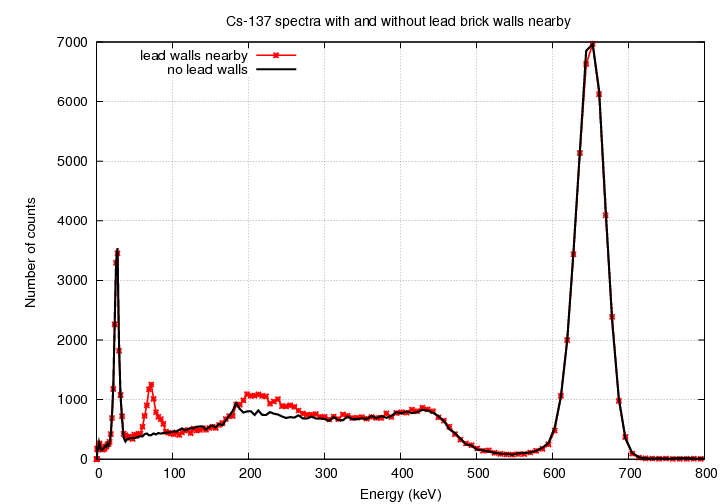
I removed the lead bricks and placed the source on an
empty cardboard box so that it was at the same distance
from the source as usual.
Look at the difference in the spectrum:
For more information
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.

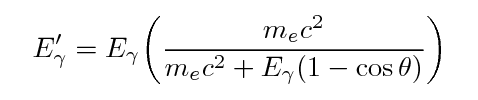
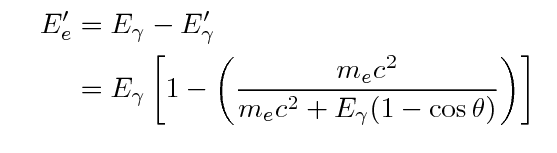
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.