Differential photometry exercise

Last modified Oct 28, 2020

This exerise involves measurements of stars in the field of the variable star IY UMa , which is at RA = 10:43:56.73, Dec = +58:07:31.9 (J2000). The chart below is based on one of the images I acquired at the RIT Observatory on Apr 11, 2006.

You can download FITS images of this field from one of my courses, if necessary (but it shouldn't be):

Directory containing FITS images of IY UMa

I've performed aperture photometry in the usual manner to measure the instrumental magnitudes of the stars "A", "B", "C", and "IY", using an aperture of radius 5 pixels. I've placed the results into a table

text file 'apr11_instr_mags.dat'

that looks something like this:



#    JD            A       B       C      IY
2453837.55043   13.5940 14.8260 14.6970 15.2840
2453837.55095   13.6820 14.9250 14.8150 15.3310
2453837.55147   13.7220 14.9170 14.8340 15.3420

where the columns are:

Julian Date
instrumental magnitude of star A
instrumental magnitude of star B
instrumental magnitude of star C
instrumental magnitude of star IY

Now it's your turn:

Make a graph which shows instrumental magnitude as a function of Julian Date, with all the stars on this single graph. Invert the y-axis so bright stars are at the top.
Which star(s) are changing in brightness? What conclusions can we draw about any intrinsic variability in IY?
Can you explain the behavior of the stars in this graph?

Now, pick star "B" as a reference. For each image individually, compute the differential magnitude between each star and "B", like so:

          diff mag A  =  mag(A)  - mag(B) 
          diff mag B  =  mag(B)  - mag(B) 
          diff mag C  =  mag(C)  - mag(B) 
          diff mag IY =  mag(IY) - mag(B)

For the first image, for example, the differential magnitudes will look like this:

       #    JD           A-B      B-B     C-B    IY-B  
       2453837.55043   -1.232    0.000  -0.129  0.458

Save these values in a new text file.

Create a single new graph which shows the differential magnitudes of all the stars as a function of Julian Date.
Look at this new graph, and again answer the question: Which star(s) are changing in brightness? What conclusions can we draw about any intrinsic variability in IY?

Now, let's do a simple sort of photometric calibration.

It might help if you refer to the following chart, which is based on the Digitized Sky Survey used by Aladin, rather than one of my RIT Observatory images.

Look up the stars A, B, and C, in the UCAC4 catalog. Write down their ID numbers and their V-band magnitudes.
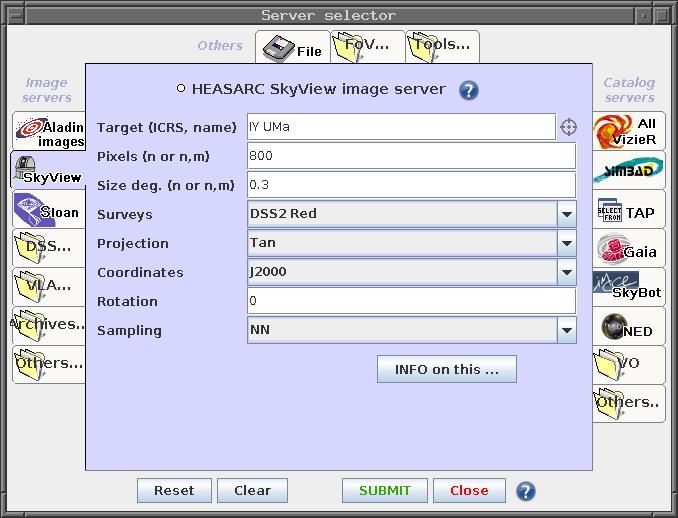
(Having trouble identifying these stars? I recommend using Aladin, then choosing "File -> Open server selector", and filling in the options so that they look like the figure below. That should give you a chart with field of view about 19 x 19 arcminutes.)
For each image, do the following:
1. compute the difference between the differential mag of each reference star and its catalog mag:
```
             delta_A = (diff mag A) - (V-band mag of A)
             delta_B = (diff mag B) - (V-band mag of B)
             delta_C = (diff mag C) - (V-band mag of C)
     
```
2. compute the average delta value for that image, which will allow us to shift the differential magnitudes to the standard V-band scale
```
             avg_delta  = (1/3) * (delta_A + delta_B + delta_C)
     
```
3. finally, subtract this average delta from differential magnitudes of each star in the image, including IY:
```
             calib_A  =  (diff mag A) - avg_delta
             calib_B  =  (diff mag B) - avg_delta
             calib_C  =  (diff mag C) - avg_delta
             calib_IY =  (diff mag IY) - avg_delta
     
```
Now you can provide other astronomers with roughly calibrated V-band magnitudes for star IY
Create a new graph, showing the light curves of all four objects converted to V-band magnitudes.

For more information

The first talk in this series was Making quantitative measurements using CCD images (I) (May 29, 2014)

The second talk in this series was Making quantitative measurements using CCD images (II) (June 20, 2014)

You can find the FITS images of IY UMa used for the exercise described in this document by visiting
http://spiff.rit.edu/classes/phys445/work/apr11_2006/
You should find 99 images, each a simple 16-bit integer FITS image, 510-by-340 pixels in size.

The UCAC4 catalog is a good choice for comparing to images taken with small telescopes and CCD cameras.
- The technical paper describing the catalog is Zacharias et al., AJ 145, 44 (2013)
- You can query the UCAC4 catalog in Vizier