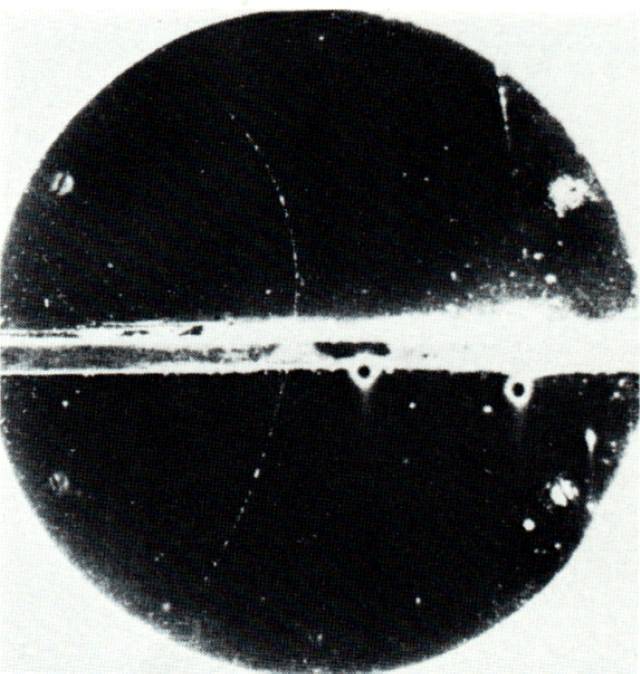
The curved path in this picture shows the track of a positron; see the full story from LBL .
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
You will occasionally need to fit a model of some sort to some measurements. Models with more parameters will give a better fit, but is it kosher to keep adding more and more parameters? When is the fit "good enough" that adding more parameters isn't really justified?
There are no exact answers to these questions, but this little guide may provide some guidance.
Joe has an electron gun and a cloud chamber. When he fires an electron into the cloud chamber, the electron ionizes air molecules, causing water vapor to condense into little droplets. The droplets trace out the path of the electron, so that Joe can measure its position at any time.

The curved path in this picture shows the track of
a positron; see
the full story from LBL .
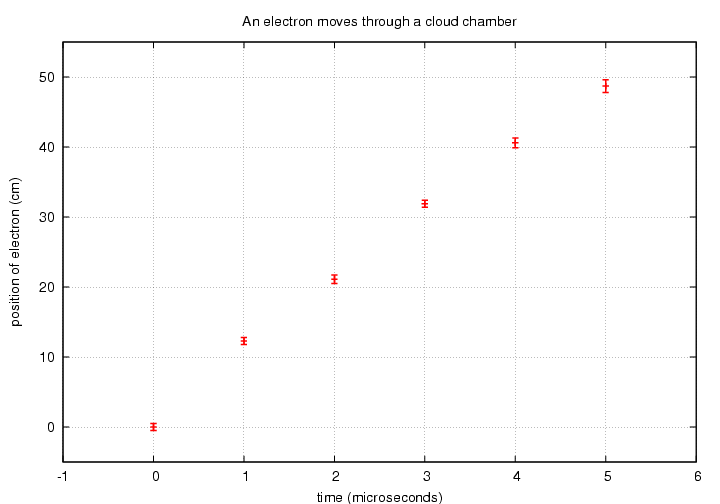
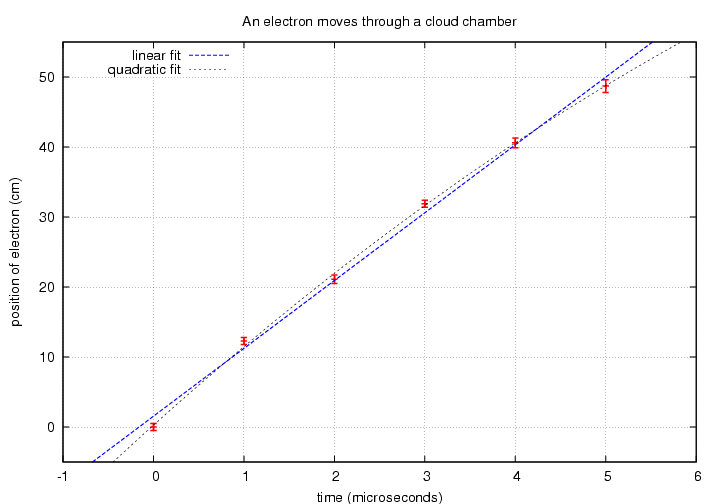
Joe uses a high-speed camera to measure the track of an electron through his chamber. He wonders -- is there a signficant electric or magnetic field inside the chamber? Here are his measurements; note the uncertainty associated with each position.
# motion of an electron in a region which # may or may not have a significant electric field # time(microsec) position(cm) pos_uncert(cm) 0.0 0 0.5 1.0 12.3 0.5 2.0 21.1 0.6 3.0 31.9 0.5 4.0 40.6 0.7 5.0 48.7 0.9
If there are no fields inside the chamber, the electron should move with constant velocity. But if there is an electric or magnetic field, the electron's velocity may change. Joe plots the position versus time to look for curvature.
"Hmmm," thinks Joe, "that looks like a pretty straight line. Let me make a linear fit, using a model with 2 parameters, a and b, like this:"
Joe finds parameters (you can read how Joe used Gnuplot to perform the fit if you wish)
a = 1.54
b = 9.69
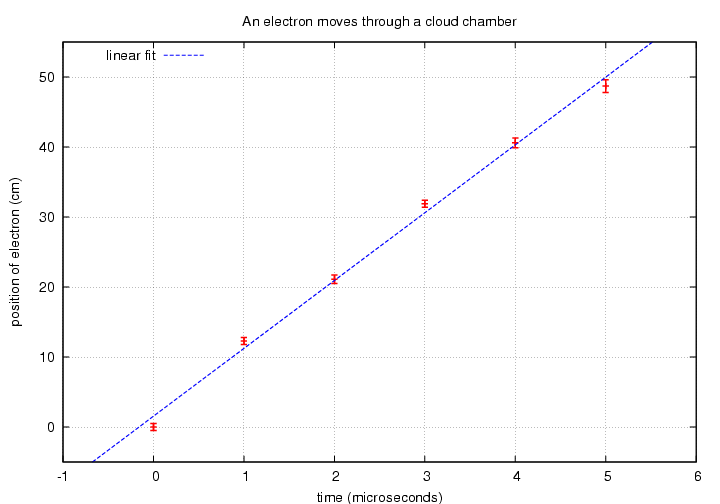
"Well, that's not bad," says Joe, "but it looks as if there might be some curvature there. Maybe I should try a quadratic fit with 3 parameters, like this:"
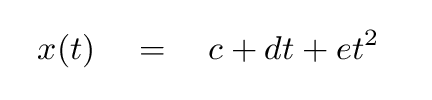
Joe finds parameters (you can read how Joe used Gnuplot to perform the fit if you wish)
c = 0.26
d = 11.60
e = -0.382
"Yes, that quadratic model is definitely better, but is it really appropriate to add one extra parameter?" wonders Joe.
There are several ways to answer that question. I'll mention two.
In the example above, there are 6 data.
By this metric, adding the extra parameter would be justified -- it brings the model into agreement with the data at the one-sigma level.
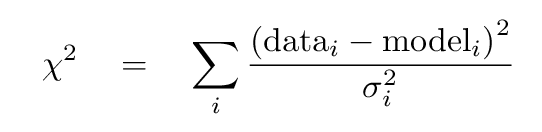
In this case, there are N=6 measurements. That means that we need to add up six terms. As an example, consider the linear model. For the first measurement, at time t = 0, it predicts model x = 1.54 cm, while the actual position was actual x = 0.0 cm. That means that the chi-squared statistic for the linear model will start like this:
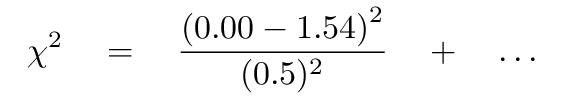
Task 1: What is the chi-squared statistic for the linear model,
if you include all 6 measurements?
We can also consider the quadratic model. For the first measurement, at time t = 0, it predicts model x = 0.26 cm, while the actual position was actual x = 0.0 cm. That means that the chi-squared statistic for the linear model will start like this:
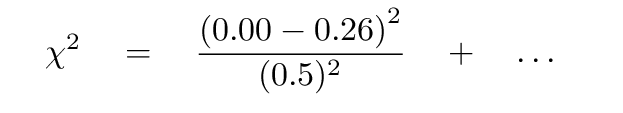
Task 2: What is the chi-squared statistic for the quadratic model,
if you include all 6 measurements?
Not surprisingly, the quadratic model yields a smaller total chi-squared value. After all, we were able to adjust an extra parameter. But -- is that decrease in the chi-squared value ENOUGH of a decrease to justify the extra parameter?
To find out, we need to account for the number of parameters in each model, and the number of measurements. We can define the number of degrees of freedom as "the number of measurements minus the number of free parameters in the model."
Task 3: What is the number of degrees of freedom
for the linear model?
What is the number of degrees of freedom
for the quadratic model?
Now, we can use the degrees of freedom to compute an adjusted value for the chi-squared statistic, which is called the reduced chi-squared statistic:
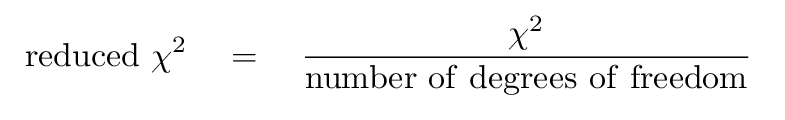
Task 4: What is the reduced chi-squared value
for the linear model?
What is the reduced chi-squared value
for the quadratic model?
Now, a general rule of thumb is that if the model is a very good fit to the measurements, the reduced chi-squared statistic will be close to 1.0. Values much larger than 1.0 mean that the model isn't a good fit, or that there are additional systematic effects which have not been accounted for in the model, or that the measurement errors might have been under-estimated, or that the errors aren't distributed in a gaussian fashion, or ... lots of other possibilities.
So, if you add one more parameter and the reduced chi-squared value decreases a LOT, then probably adding that parameter was a good idea. If the reduced chi-squared value only decreases by a small amount, then adding that extra parameter probably wasn't justified.
Task 5: In this case, do you think that
going from a linear model to a
quadratic table was justified?
This page maintained by Michael Richmond. Last modified Apr 8, 2009.
 Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.
Copyright © Michael Richmond.
This work is licensed under a Creative Commons License.